Математические методы – задачи – 10 вариант
Количество страниц: 20
Графические материалы: 8 рисунков, 7 таблиц
Кол-во источников литературы: 5
ЗАДАНИЕ № 1.
Тема: «Выпуклое программирование»
Предприятие выпускает изделия А и Б, при изготовлении которых используется сырье и . Известны:
Как только объем выпускаемой продукции перестает соответствовать оптимальным размерам предприятия, дальнейшее увеличение выпуска ведет к повышению себестоимости продукции и в первом приближении фактическая себестоимость описывается функцией , где – некоторая постоянная величина. При поиске плана выпуска изделий, обеспечивающего предприятию наивысшую прибыль в условиях нарушения баланса между объемом выпуска и оптимальными размерами предприятия, целевая функция принимает вид:
а ограничения по сырью:
Требуется:
1) составить математическую модель задачи применительно к числовым данным выполняемого варианта;
2) графическим методом решить полученную задачу и сформулировать ответ в экономических терминах в соответствии с условиями задачи.
Решение:
[……]
ЗАДАНИЕ №2.
Тема: «Программирование на сетях»
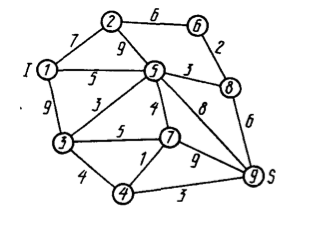
На заданной сети указаны пропускные способности ребер. Предполагается, что пропускные способности в обоих направлениях одинаковы.
Требуется:
1) сформировать на сети поток максимальной мощности, направленный из истока I в сток S;
2) выписать ребра, образующие на сети разрез минимальной пропускной способности.
Решение:
[……]
ЗАДАНИЕ №3.
Тема: «Динамическое программирование»
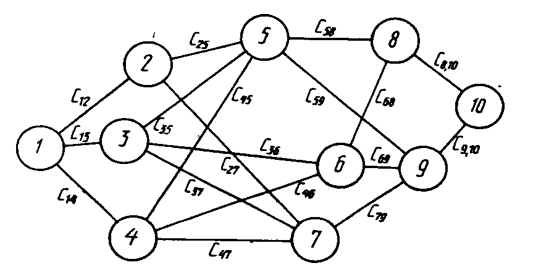
На данной сети дорог имеется несколько маршрутов, по которым можно доставлять груз из пункта 1 в пункт 10:
Известны стоимости сij перевозки единицы груза между пунктами сети. Требуется:
1) методом динамического программирования найти на сети наиболее экономный маршрут доставки груза из пункта 1 в пункт 10 и соответствующие ему затраты;
2) выписать оптимальные маршруты перевозки груза из всех остальных пунктов сети в пункт 10 и указать отвечающие им минимальные затраты на доставку.
Числовые данные:
Решение:
[……]
ЗАДАНИЕ №4.
Тема «Элементы теории матричных игр»
После нескольких лет эксплуатации промышленное оборудование оказывается в одном из следующих состояний: B1 – оборудование может использоваться в очередном году после профилактического ремонта; В2 – для безаварийной работы оборудования в дальнейшем следует заменить отдельные его детали и узлы; В3 – оборудование требует капитального ремонта или замены.
В зависимости от сложившейся ситуации B1, B2, B3 руководство предприятия может принять такие решения: A1 – отремонтировать оборудование силами заводских специалистов, что потребует соответствующих затрат , , ден. ед.; A2 – вызвать специальную бригаду ремонтников, расходы в этом случае составят , , ден.ед.; A3 – заменить оборудование новым, реализовав устаревшее оборудование по его остаточной стоимости. Совокупные затраты в результате этого мероприятия будут равны соответственно , , ден. ед.
Задание:
- Придав описанной ситуации игровую схему, выявить ее участников, указать возможные чистые стратегии сторон.
- Составить платежную матрицу, пояснив смысл элементов матрицы (почему они отрицательные?).
- Выяснить, какое решение о работе оборудования в предстоящем году целесообразно рекомендовать руководству предприятия, чтобы минимизировать потери при следующих предположениях:
а) накопленный на предприятии опыт эксплуатации аналогичного оборудования показывает, что вероятности указанных состояний оборудования равны соответственно , , (примените критерий Байеса);
б) имеющийся опыт свидетельствует о том, что все три возможных состояния оборудования равновероятны (примените критерий Лапласа);
в) о вероятностях оборудования ничего определенного сказать нельзя (примените критерии Вальда, Сэвиджа, Гурвица). Значение параметра γ=0,7.
Решение:
[……]
При обращении ОБЯЗАТЕЛЬНО напишите индивидуальный номер работы – указан в самом верху.

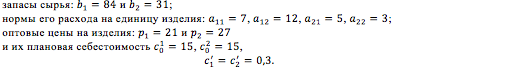

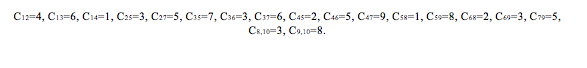
— Дина, г. Москва
работа отличная,спасибоооо
— Щерб…ва Юлия
— Д.И.
Доброе утро!
Спасибо Вам огромное за Ваш профессионализм!
Защитилась на 5 😊
— Андрей К.
Добрый день) Курсовую работу защитил, все отлично) спасибо.
Скоро напишу Вам по дипломной работе. Там работа должна быть скоординирована с лабораторной работой у Анны Николаевны Жилкиной, ну вы знаете )